Awaken Audiences
Umfassende Consumer Insights für eine optimierte Kampagnen-Performance.
Ganzheitlicher Ansatz der Zielgruppenanalyse
Von Consumer Insights zur Media-Aktivierung.
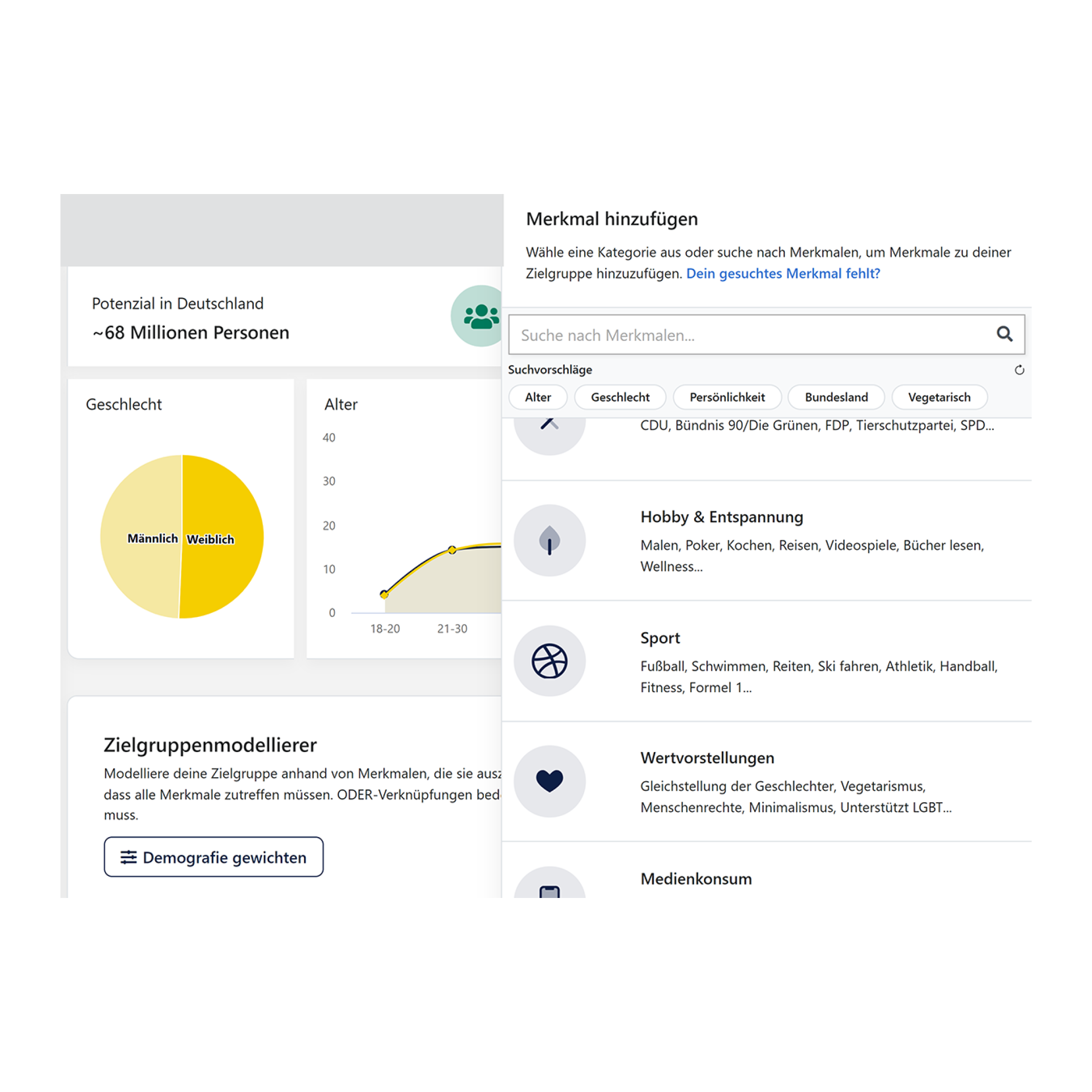
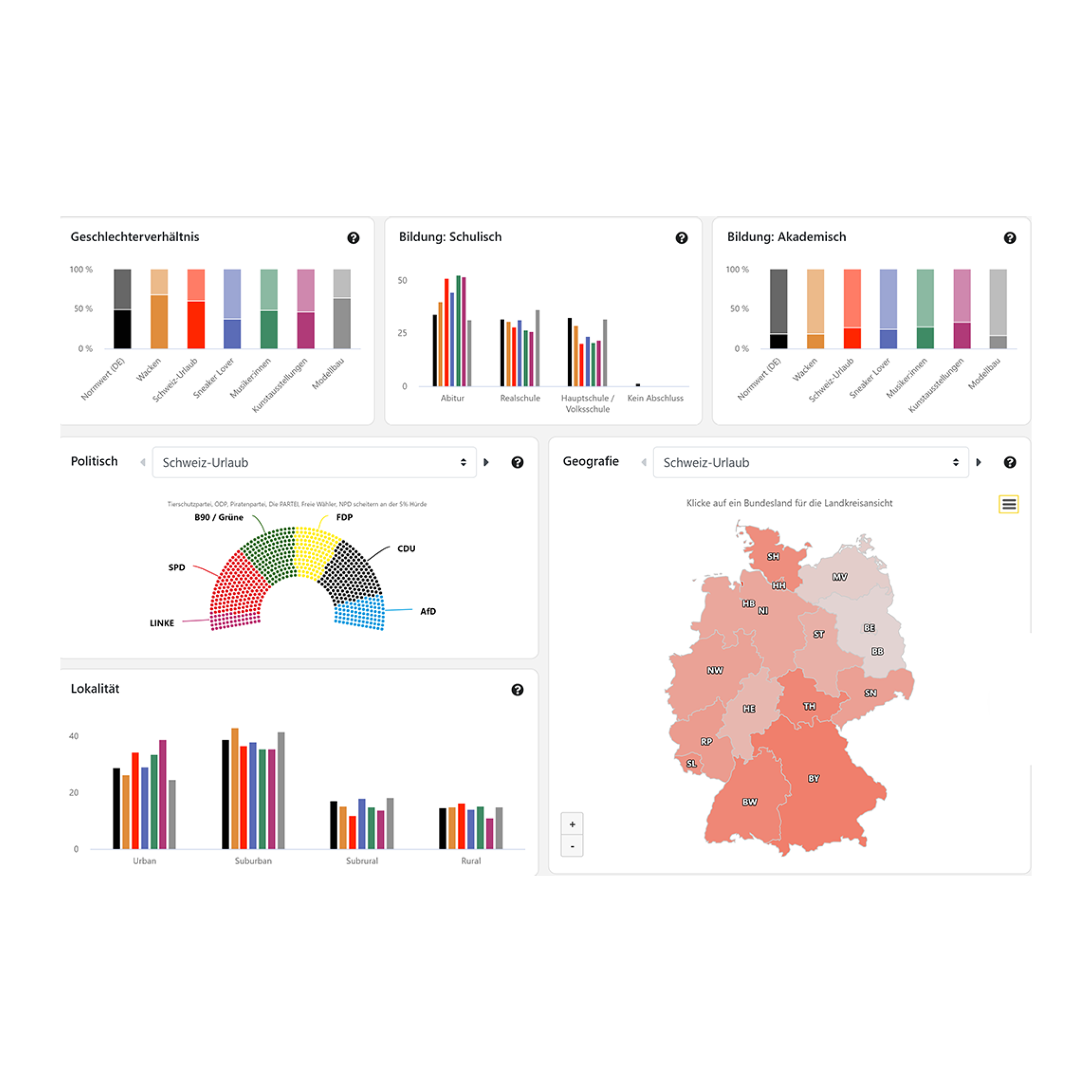
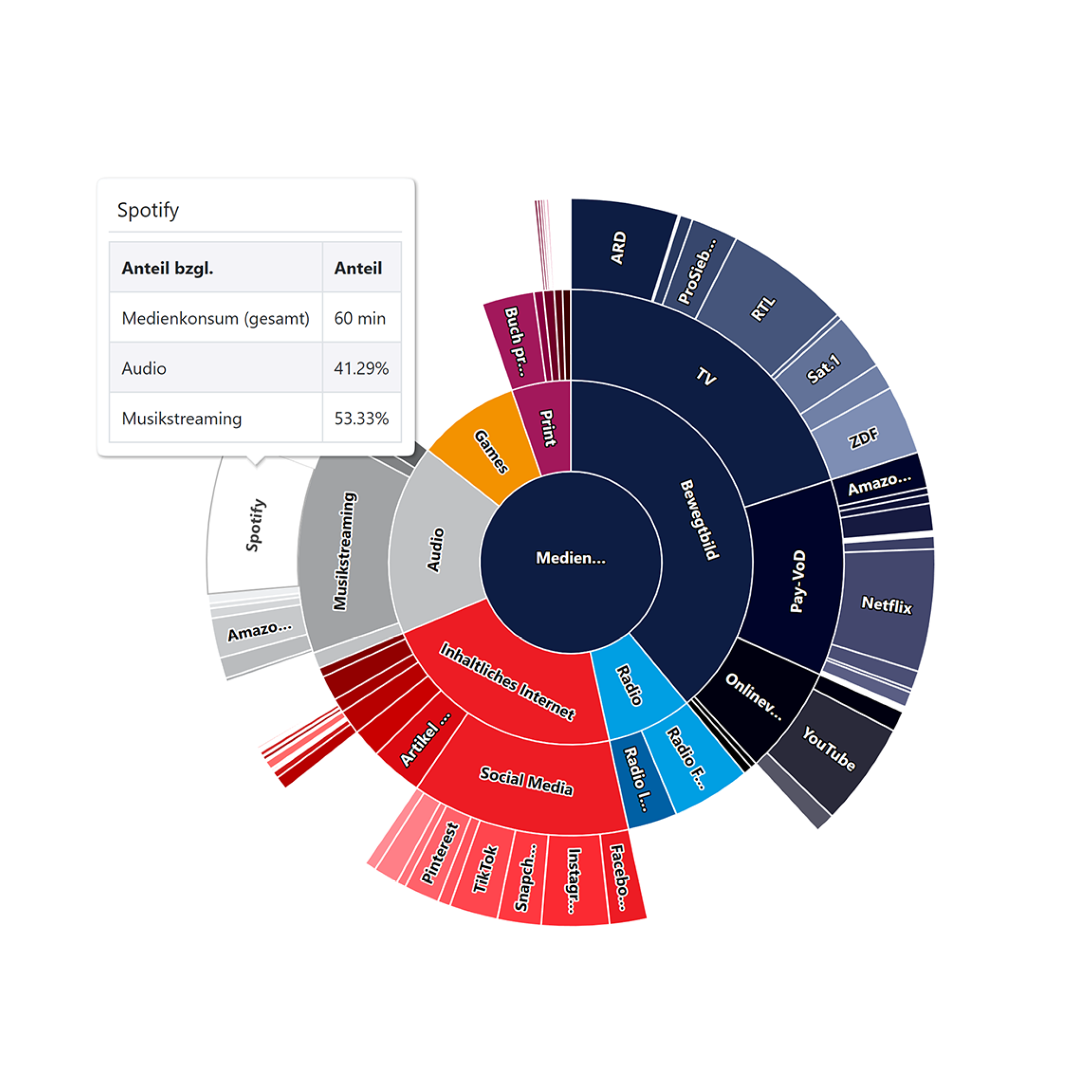
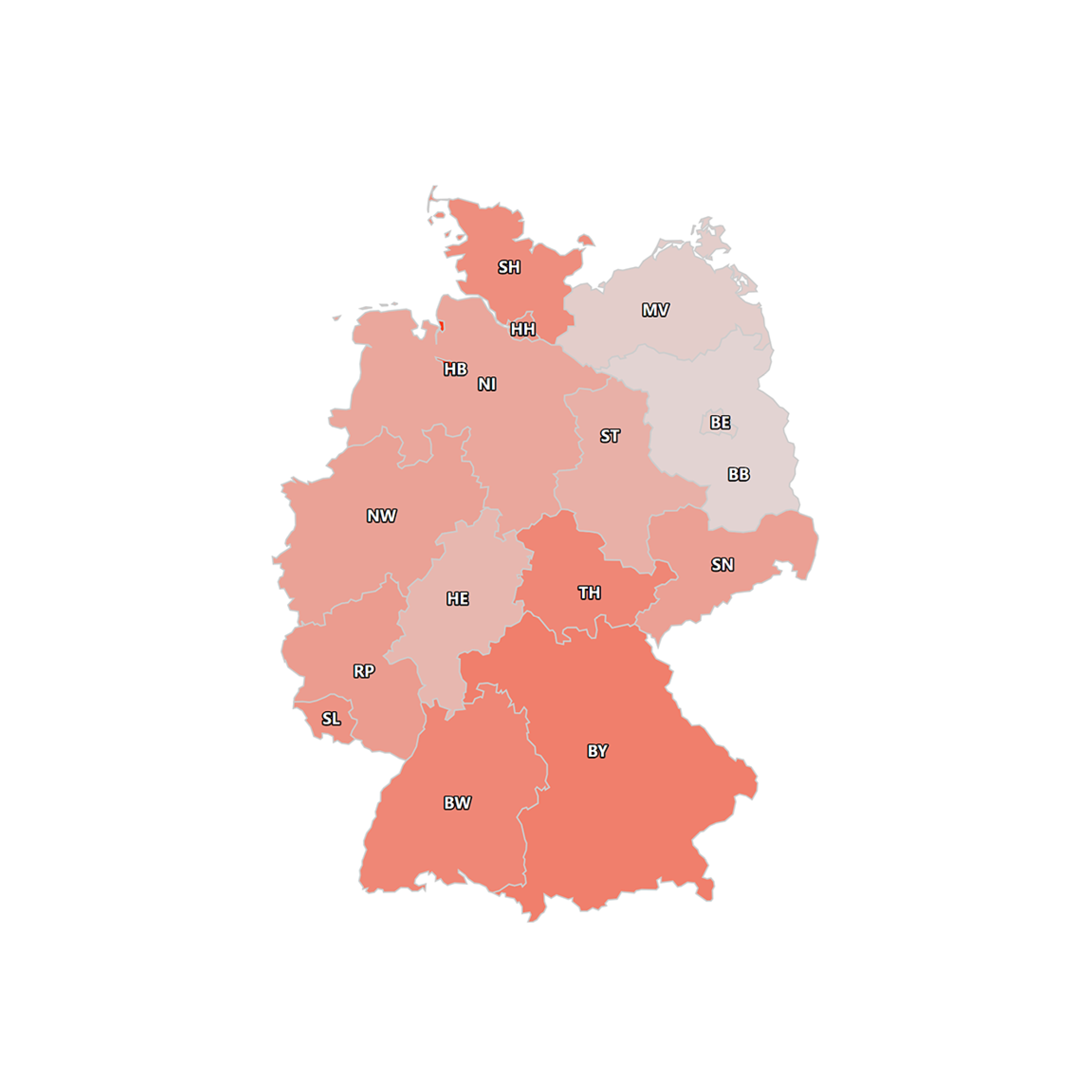
AIlon, die Flagship-KI von ERASON, generiert auf Basis von Big Data die umfangreichste Marktmedia-Studie in Deutschland und ermöglicht so agile Marktforschung und automatisierte Mediaplanung auf Knopfdruck – ganz ohne Umfragen.
Werbetreibende erhalten in kürzester Zeit tiefgreifende Zielgruppen-Insights, um datengestützt die Performance ihrer Kampagnen zu optimieren und massive Kosteneinsparungen in der Mediaplanung zu realisieren.
Ergebnisse, die überzeugen
In Kunden-Cases konnten wir durchschnittlich die KPIs im zweistelligen Prozentbereich verbessern.
-40%
Cost per Order
Programmatic
-21%
Cost per Lead
Meta
-11%
Cost per Lead
Von führenden Unternehmen genutzt
Und als Hochtechnologie-Startup vom Bundeswirtschaftsministerium und der EU gefördert.








Kundenstimmen



Gute Gründe für AIlon
Mit kohärenten Analysedaten für Konzeption, Kreation und Targeting lassen sich enorme Effektivitäts- und Effizienzsteigerungen in der Marketing-Kommunikations- und Mediaplanung realisieren.
Customer Centricity leben
Profiliere dein Angebot und stelle Relevanz und Involvement durch passgenaue Ansprache sicher.
Massiv Kosten senken
Minimiere Streuverluste und optimiere deine Mediaplanung dank präzisester, crossmedialer Targeting- und Budgetempfehlungen.
Zielgruppe in Media übersetzen
Realisiere Konzepte in Media. Der manuelle Übersetzungsprozess entfällt durch die gemeinsame Datenbasis.
Agilität ermöglichen
Setze dich konsequent mit deiner Zielgruppe auseinander und treffe datengestützt operative und strategische Entscheidungen.